Idealised 2-D viscoelastic loading problem in an annulus¶

In this tutorial, we examine an idealised 2-D loading problem in an annulus domain.

This example focusses on differences between running simulations in a 2-D annulus and 2-D Cartesian domain. These can be summarised as follows:

1. The geometry of the problem - i.e. the computational mesh.
2. The radial direction of gravity (as opposed to the vertical direction in a Cartesian domain).
3. Solving a problem with laterally varying viscosity.
4. Accounting for a (rotational) velocity nullspace.

This example¶

Let's get started! The first step is to import the gadopt module, which provides access to Firedrake and associated functionality.

In [1]:

from gadopt import *
from gadopt.utility import step_func, vertical_component

from gadopt import * from gadopt.utility import step_func, vertical_component

We generate a circular manifold mesh (with 180 elements) and extrude in the radial direction, using the optional keyword argument extrusion_type, forming 32 layers. To better represent the curvature of the domain and ensure accuracy of our quadratic representation of incremental displacement, we approximate the curved cylindrical shell domain quadratically, using the optional keyword argument degree$=2$.

As this problem is not formulated in a Cartesian geometry we set the mesh.cartesian attribute to False. This ensures the correct configuration of a radially inward vertical direction.

In [2]:

# Set up geometry:
rmin = 3480e3
rmax = 6371e3
D = rmax-rmin
nz = 32
ncells = 180
dz = D / nz

# Construct a circle mesh and then extrude into a cylinder:
surface_mesh = CircleManifoldMesh(ncells, radius=rmin, degree=2, name='surface_mesh')
mesh = ExtrudedMesh(surface_mesh, layers=nz, layer_height=dz, extrusion_type='radial')

bottom_id, top_id = "bottom", "top"
mesh.cartesian = False

# Set up geometry: rmin = 3480e3 rmax = 6371e3 D = rmax-rmin nz = 32 ncells = 180 dz = D / nz # Construct a circle mesh and then extrude into a cylinder: surface_mesh = CircleManifoldMesh(ncells, radius=rmin, degree=2, name='surface_mesh') mesh = ExtrudedMesh(surface_mesh, layers=nz, layer_height=dz, extrusion_type='radial') bottom_id, top_id = "bottom", "top" mesh.cartesian = False

We next set up the function spaces, and specify functions to hold our solutions.

In [3]:

# Set up function spaces - currently using the bilinear Q2Q1 element pair:
V = VectorFunctionSpace(mesh, "CG", 2)  # (Incremental) Displacement function space (vector)
W = FunctionSpace(mesh, "CG", 1)  # Pressure function space (scalar)
S = TensorFunctionSpace(mesh, "DQ", 2)  # (Discontinuous) Stress tensor function space (tensor)
R = FunctionSpace(mesh, "R", 0)  # Real function space (for constants)

Z = MixedFunctionSpace([V, W])  # Mixed function space.

z = Function(Z)  # A field over the mixed function space Z.
u, p = split(z)  # Returns symbolic UFL expression for u and p
z.subfunctions[0].rename("Incremental Displacement")
z.subfunctions[1].rename("Pressure")

displacement = Function(V, name="displacement").assign(0)
stress_old = Function(S, name="stress_old").assign(0)

# Set up function spaces - currently using the bilinear Q2Q1 element pair: V = VectorFunctionSpace(mesh, "CG", 2) # (Incremental) Displacement function space (vector) W = FunctionSpace(mesh, "CG", 1) # Pressure function space (scalar) S = TensorFunctionSpace(mesh, "DQ", 2) # (Discontinuous) Stress tensor function space (tensor) R = FunctionSpace(mesh, "R", 0) # Real function space (for constants) Z = MixedFunctionSpace([V, W]) # Mixed function space. z = Function(Z) # A field over the mixed function space Z. u, p = split(z) # Returns symbolic UFL expression for u and p z.subfunctions[0].rename("Incremental Displacement") z.subfunctions[1].rename("Pressure") displacement = Function(V, name="displacement").assign(0) stress_old = Function(S, name="stress_old").assign(0)

We can output function space information, for example the number of degrees of freedom (DOF).

In [4]:

# Output function space information:
log("Number of Incremental Displacement DOF:", V.dim())
log("Number of Pressure DOF:", W.dim())
log("Number of Velocity and Pressure DOF:", V.dim()+W.dim())

# Output function space information: log("Number of Incremental Displacement DOF:", V.dim()) log("Number of Pressure DOF:", W.dim()) log("Number of Velocity and Pressure DOF:", V.dim()+W.dim())

Number of Incremental Displacement DOF: 46800
Number of Pressure DOF: 5940
Number of Velocity and Pressure DOF: 52740

We can now visualise the resulting mesh.

In [5]:

active-ipynb

import pyvista as pv
import matplotlib.pyplot as plt

VTKFile("mesh.pvd").write(Function(V))
mesh_data = pv.read("mesh/mesh_0.vtu")
edges = mesh_data.extract_all_edges()
plotter = pv.Plotter(notebook=True)
plotter.add_mesh(edges, color="black")
plotter.camera_position = "xy"
plotter.show(jupyter_backend="static", interactive=False)

import pyvista as pv import matplotlib.pyplot as plt VTKFile("mesh.pvd").write(Function(V)) mesh_data = pv.read("mesh/mesh_0.vtu") edges = mesh_data.extract_all_edges() plotter = pv.Plotter(notebook=True) plotter.add_mesh(edges, color="black") plotter.camera_position = "xy" plotter.show(jupyter_backend="static", interactive=False)

Let's start initialising some parameters. First of all let's get the (symbolic) spatial coordinates of the mesh

In [6]:

X = SpatialCoordinate(mesh)

X = SpatialCoordinate(mesh)

Now we can set up the background profiles for the material properties. In this case the density and shear modulus vary in the vertical direction. We will approximate the series of layers using a smooth tanh function with a width of 40 km. The layer properties specified are from spada et al. (2011). N.b. that we have modified the viscosity of the Lithosphere viscosity from Spada et al. (2011) because we are using coarse grid resolution.

In [7]:

radius_values = [6371e3, 6301e3, 5951e3, 5701e3]
density_values = [3037, 3438, 3871, 4978]
shear_modulus_values = [0.50605e11, 0.70363e11, 1.05490e11, 2.28340e11]
viscosity_values = [2, -2, -2, -1.698970004]  # viscosity = 1e23 * 10**viscosity_values


def initialise_background_field(field, background_values, vertical_tanh_width=40e3):
    profile = background_values[0]
    sharpness = 1 / vertical_tanh_width
    depth = sqrt(X[0]**2 + X[1]**2)-radius_values[0]
    for i in range(1, len(background_values)):
        centre = radius_values[i] - radius_values[0]
        mag = background_values[i] - background_values[i-1]
        profile += step_func(depth, centre, mag, increasing=False, sharpness=sharpness)

    field.interpolate(profile)


density = Function(W, name="density")
initialise_background_field(density, density_values)

shear_modulus = Function(W, name="shear modulus")
initialise_background_field(shear_modulus, shear_modulus_values)

radius_values = [6371e3, 6301e3, 5951e3, 5701e3] density_values = [3037, 3438, 3871, 4978] shear_modulus_values = [0.50605e11, 0.70363e11, 1.05490e11, 2.28340e11] viscosity_values = [2, -2, -2, -1.698970004] # viscosity = 1e23 * 10**viscosity_values def initialise_background_field(field, background_values, vertical_tanh_width=40e3): profile = background_values[0] sharpness = 1 / vertical_tanh_width depth = sqrt(X[0]**2 + X[1]**2)-radius_values[0] for i in range(1, len(background_values)): centre = radius_values[i] - radius_values[0] mag = background_values[i] - background_values[i-1] profile += step_func(depth, centre, mag, increasing=False, sharpness=sharpness) field.interpolate(profile) density = Function(W, name="density") initialise_background_field(density, density_values) shear_modulus = Function(W, name="shear modulus") initialise_background_field(shear_modulus, shear_modulus_values)

Let's have a quick look at the density field using pyvista.

In [8]:

active-ipynb

# Read the PVD file
density_file = VTKFile('density.pvd').write(density)
reader = pv.get_reader("density.pvd")
data = reader.read()[0]  # MultiBlock mesh with only 1 block

# Create a plotter object
plotter = pv.Plotter(shape=(1, 1), border=False, notebook=True, off_screen=False)

# Make a colour map
boring_cmap = plt.get_cmap("viridis", 25)
# Add the warped displacement field to the frame
plotter.add_mesh(
    data,
    component=None,
    lighting=False,
    show_edges=False,
    cmap=boring_cmap,
    scalar_bar_args={
        "title": 'Density (kg / m^3)',
        "position_x": 0.8,
        "position_y": 0.2,
        "vertical": True,
        "title_font_size": 20,
        "label_font_size": 16,
        "fmt": "%.0f",
        "font_family": "arial",
    }
)
plotter.camera_position = 'xy'
plotter.show(jupyter_backend="static", interactive=False)
# Closes and finalizes movie
plotter.close()

# Read the PVD file density_file = VTKFile('density.pvd').write(density) reader = pv.get_reader("density.pvd") data = reader.read()[0] # MultiBlock mesh with only 1 block # Create a plotter object plotter = pv.Plotter(shape=(1, 1), border=False, notebook=True, off_screen=False) # Make a colour map boring_cmap = plt.get_cmap("viridis", 25) # Add the warped displacement field to the frame plotter.add_mesh( data, component=None, lighting=False, show_edges=False, cmap=boring_cmap, scalar_bar_args={ "title": 'Density (kg / m^3)', "position_x": 0.8, "position_y": 0.2, "vertical": True, "title_font_size": 20, "label_font_size": 16, "fmt": "%.0f", "font_family": "arial", } ) plotter.camera_position = 'xy' plotter.show(jupyter_backend="static", interactive=False) # Closes and finalizes movie plotter.close()

Next let's initialise the viscosity field. In this tutorial we are going to make things a bit more interesting by using a laterally varying viscosity field. We'll put some regions of low viscosity near the South Pole (inspired by West Antarctica) as well as in the lower mantle. We've also put some relatively higher viscosity patches of mantle in the northern hemisphere to represent a downgoing slab.

In [9]:

def bivariate_gaussian(x, y, mu_x, mu_y, sigma_x, sigma_y, rho, normalised_area=False):
    arg = ((x-mu_x)/sigma_x)**2 - 2*rho*((x-mu_x)/sigma_x)*((y-mu_y)/sigma_y) + ((y-mu_y)/sigma_y)**2
    numerator = exp(-1/(2*(1-rho**2))*arg)
    if normalised_area:
        denominator = 2*pi*sigma_x*sigma_y*(1-rho**2)**0.5
    else:
        denominator = 1
    return numerator / denominator


def setup_heterogenous_viscosity(viscosity):
    heterogenous_viscosity_field = Function(viscosity.function_space(), name='viscosity')
    antarctica_x, antarctica_y = -2e6, -5.5e6

    low_viscosity_antarctica = bivariate_gaussian(X[0], X[1], antarctica_x, antarctica_y, 1.5e6, 0.5e6, -0.4)
    heterogenous_viscosity_field.interpolate(-3*low_viscosity_antarctica + viscosity * (1-low_viscosity_antarctica))

    llsvp1_x, llsvp1_y = 3.5e6, 0
    llsvp1 = bivariate_gaussian(X[0], X[1], llsvp1_x, llsvp1_y, 0.75e6, 1e6, 0)
    heterogenous_viscosity_field.interpolate(-3*llsvp1 + heterogenous_viscosity_field * (1-llsvp1))

    llsvp2_x, llsvp2_y = -3.5e6, 0
    llsvp2 = bivariate_gaussian(X[0], X[1], llsvp2_x, llsvp2_y, 0.75e6, 1e6, 0)
    heterogenous_viscosity_field.interpolate(-3*llsvp2 + heterogenous_viscosity_field * (1-llsvp2))

    slab_x, slab_y = 3e6, 4.5e6
    slab = bivariate_gaussian(X[0], X[1], slab_x, slab_y, 0.7e6, 0.35e6, 0.7)
    heterogenous_viscosity_field.interpolate(-1*slab + heterogenous_viscosity_field * (1-slab))

    high_viscosity_craton_x, high_viscosity_craton_y = 0, 6.2e6
    high_viscosity_craton = bivariate_gaussian(X[0], X[1], high_viscosity_craton_x, high_viscosity_craton_y, 1.5e6, 0.5e6, 0.2)
    heterogenous_viscosity_field.interpolate(-1*high_viscosity_craton + heterogenous_viscosity_field * (1-high_viscosity_craton))

    return heterogenous_viscosity_field


normalised_viscosity = Function(W, name="Normalised viscosity")
initialise_background_field(normalised_viscosity, viscosity_values)
normalised_viscosity = setup_heterogenous_viscosity(normalised_viscosity)

viscosity = Function(normalised_viscosity, name="viscosity").interpolate(1e23*10**normalised_viscosity)

def bivariate_gaussian(x, y, mu_x, mu_y, sigma_x, sigma_y, rho, normalised_area=False): arg = ((x-mu_x)/sigma_x)**2 - 2*rho*((x-mu_x)/sigma_x)*((y-mu_y)/sigma_y) + ((y-mu_y)/sigma_y)**2 numerator = exp(-1/(2*(1-rho**2))*arg) if normalised_area: denominator = 2*pi*sigma_x*sigma_y*(1-rho**2)**0.5 else: denominator = 1 return numerator / denominator def setup_heterogenous_viscosity(viscosity): heterogenous_viscosity_field = Function(viscosity.function_space(), name='viscosity') antarctica_x, antarctica_y = -2e6, -5.5e6 low_viscosity_antarctica = bivariate_gaussian(X[0], X[1], antarctica_x, antarctica_y, 1.5e6, 0.5e6, -0.4) heterogenous_viscosity_field.interpolate(-3*low_viscosity_antarctica + viscosity * (1-low_viscosity_antarctica)) llsvp1_x, llsvp1_y = 3.5e6, 0 llsvp1 = bivariate_gaussian(X[0], X[1], llsvp1_x, llsvp1_y, 0.75e6, 1e6, 0) heterogenous_viscosity_field.interpolate(-3*llsvp1 + heterogenous_viscosity_field * (1-llsvp1)) llsvp2_x, llsvp2_y = -3.5e6, 0 llsvp2 = bivariate_gaussian(X[0], X[1], llsvp2_x, llsvp2_y, 0.75e6, 1e6, 0) heterogenous_viscosity_field.interpolate(-3*llsvp2 + heterogenous_viscosity_field * (1-llsvp2)) slab_x, slab_y = 3e6, 4.5e6 slab = bivariate_gaussian(X[0], X[1], slab_x, slab_y, 0.7e6, 0.35e6, 0.7) heterogenous_viscosity_field.interpolate(-1*slab + heterogenous_viscosity_field * (1-slab)) high_viscosity_craton_x, high_viscosity_craton_y = 0, 6.2e6 high_viscosity_craton = bivariate_gaussian(X[0], X[1], high_viscosity_craton_x, high_viscosity_craton_y, 1.5e6, 0.5e6, 0.2) heterogenous_viscosity_field.interpolate(-1*high_viscosity_craton + heterogenous_viscosity_field * (1-high_viscosity_craton)) return heterogenous_viscosity_field normalised_viscosity = Function(W, name="Normalised viscosity") initialise_background_field(normalised_viscosity, viscosity_values) normalised_viscosity = setup_heterogenous_viscosity(normalised_viscosity) viscosity = Function(normalised_viscosity, name="viscosity").interpolate(1e23*10**normalised_viscosity)

Now let's plot the normalised viscosity viscosity field in log space (we have divided the viscosity by 1x10$^{23}$ Pa s). Although we are using a fairly coarse mesh we are able to capture the key features of the viscosity field.

In [10]:

active-ipynb

# Read the PVD file
visc_file = VTKFile('viscosity.pvd').write(normalised_viscosity)
reader = pv.get_reader("viscosity.pvd")
data = reader.read()[0]  # MultiBlock mesh with only 1 block

# Create a plotter object
plotter = pv.Plotter(shape=(1, 1), border=False, notebook=True, off_screen=False)

# Make a colour map
boring_cmap = plt.get_cmap("inferno_r", 25)
# Add the warped displacement field to the frame
plotter.add_mesh(
    data,
    component=None,
    lighting=False,
    show_edges=False,
    cmap=boring_cmap,
    scalar_bar_args={
        "title": 'Normalised viscosity',
        "position_x": 0.8,
        "position_y": 0.2,
        "vertical": True,
        "title_font_size": 20,
        "label_font_size": 16,
        "fmt": "%.0f",
        "font_family": "arial",
    }
)
plotter.camera_position = 'xy'
plotter.show(jupyter_backend="static", interactive=False)
# Closes and finalizes movie
plotter.close()

# Read the PVD file visc_file = VTKFile('viscosity.pvd').write(normalised_viscosity) reader = pv.get_reader("viscosity.pvd") data = reader.read()[0] # MultiBlock mesh with only 1 block # Create a plotter object plotter = pv.Plotter(shape=(1, 1), border=False, notebook=True, off_screen=False) # Make a colour map boring_cmap = plt.get_cmap("inferno_r", 25) # Add the warped displacement field to the frame plotter.add_mesh( data, component=None, lighting=False, show_edges=False, cmap=boring_cmap, scalar_bar_args={ "title": 'Normalised viscosity', "position_x": 0.8, "position_y": 0.2, "vertical": True, "title_font_size": 20, "label_font_size": 16, "fmt": "%.0f", "font_family": "arial", } ) plotter.camera_position = 'xy' plotter.show(jupyter_backend="static", interactive=False) # Closes and finalizes movie plotter.close()

Now let's setup the ice load. For this tutorial we will have two synthetic ice sheets. Let's put one a larger one over the South Pole, with a total horizontal extent of 40 $^\circ$ and a maximum thickness of 2 km, and a smaller one offset from the North Pole with a width of 20 $^\circ$ and a maximum thickness of 1 km. To simplify things let's keep the ice load fixed in time.

In [11]:

rho_ice = 931
g = 9.8125
Hice1 = 1000
Hice2 = 2000
year_in_seconds = Constant(3600 * 24 * 365.25)
# Disc ice load but with a smooth transition given by a tanh profile
disc_halfwidth1 = (2*pi/360) * 10  # Disk half width in radians
disc_halfwidth2 = (2*pi/360) * 20  # Disk half width in radians
surface_dx = 200*1e3
ncells = 2*pi*radius_values[0] / surface_dx
surface_resolution_radians = 2*pi / ncells
colatitude = atan2(X[0], X[1])
disc1_centre = (2*pi/360) * 25  # centre of disc1
disc2_centre = pi  # centre of disc2
disc1 = 0.5*(1-tanh((abs(colatitude-disc1_centre) - disc_halfwidth1) / (2*surface_resolution_radians)))
disc2 = 0.5*(1-tanh((abs(abs(colatitude)-disc2_centre) - disc_halfwidth2) / (2*surface_resolution_radians)))
ice_load = rho_ice * g * (Hice1 * disc1 + Hice2 * disc2)

rho_ice = 931 g = 9.8125 Hice1 = 1000 Hice2 = 2000 year_in_seconds = Constant(3600 * 24 * 365.25) # Disc ice load but with a smooth transition given by a tanh profile disc_halfwidth1 = (2*pi/360) * 10 # Disk half width in radians disc_halfwidth2 = (2*pi/360) * 20 # Disk half width in radians surface_dx = 200*1e3 ncells = 2*pi*radius_values[0] / surface_dx surface_resolution_radians = 2*pi / ncells colatitude = atan2(X[0], X[1]) disc1_centre = (2*pi/360) * 25 # centre of disc1 disc2_centre = pi # centre of disc2 disc1 = 0.5*(1-tanh((abs(colatitude-disc1_centre) - disc_halfwidth1) / (2*surface_resolution_radians))) disc2 = 0.5*(1-tanh((abs(abs(colatitude)-disc2_centre) - disc_halfwidth2) / (2*surface_resolution_radians))) ice_load = rho_ice * g * (Hice1 * disc1 + Hice2 * disc2)

Let's visualise the ice thickness using pyvista, by plotting a ring outside our synthetic Earth.

In [12]:

active-ipynb

def make_ice_ring(reader):
    data = reader.read()[0]

    normal = [0, 0, 1]
    polar = [rmax-dz/2, 0, 0]
    center = [0, 0, 0]
    angle = 360.0
    res = 10000
    arc = pv.CircularArcFromNormal(center, res, normal, polar, angle)

    arc_data = arc.sample(data)

    # Stretch line by 20%
    transform_matrix = np.array(
        [
            [1.2, 0, 0, 0],
            [0, 1.2, 0, 0],
            [0, 0, 1.2, 0],
            [0, 0, 0, 1],
        ]
    )
    return arc_data.transform(transform_matrix)


def plot_ice_ring(plotter, ice_ring, scalar="Ice thickness"):
    ice_cmap = plt.get_cmap("Blues", 25)

    plotter.add_mesh(
        ice_ring,
        scalars=scalar,
        line_width=10,
        cmap=ice_cmap,
        clim=[0, 2000],
        scalar_bar_args={
            "title": 'Ice thickness (m)',
            "position_x": 0.05,
            "position_y": 0.3,
            "vertical": True,
            "title_font_size": 20,
            "label_font_size": 16,
            "fmt": "%.0f",
            "font_family": "arial",
        }
    )


# Write ice thicknesss .pvd file
ice_thickness = Function(W, name="Ice thickness").interpolate(Hice1 * disc1 + Hice2 * disc2)
zero_ice_thickness = Function(W, name="zero").assign(0)  # Used for plotting later
ice_thickness_file = VTKFile('ice.pvd').write(ice_thickness, zero_ice_thickness)

ice_reader = pv.get_reader("ice.pvd")
ice_ring = make_ice_ring(ice_reader)

reader = pv.get_reader("viscosity.pvd")
data = reader.read()[0]  # MultiBlock mesh with only 1 block

# Create a plotter object
plotter = pv.Plotter(shape=(1, 1), border=False, notebook=True, off_screen=False)

# Make a colour map
boring_cmap = plt.get_cmap("inferno_r", 25)
# Add the warped displacement field to the frame
plotter.add_mesh(
    data,
    component=None,
    scalars=None,
    lighting=False,
    show_edges=False,
    cmap=boring_cmap,
    scalar_bar_args={
        "title": 'Normalised viscosity',
        "position_x": 0.8,
        "position_y": 0.3,
        "vertical": True,
        "title_font_size": 20,
        "label_font_size": 16,
        "fmt": "%.0f",
        "font_family": "arial",
    }
)

plot_ice_ring(plotter, ice_ring)

plotter.camera_position = 'xy'
plotter.show(jupyter_backend="static", interactive=False)
# Closes and finalizes movie
plotter.close()

def make_ice_ring(reader): data = reader.read()[0] normal = [0, 0, 1] polar = [rmax-dz/2, 0, 0] center = [0, 0, 0] angle = 360.0 res = 10000 arc = pv.CircularArcFromNormal(center, res, normal, polar, angle) arc_data = arc.sample(data) # Stretch line by 20% transform_matrix = np.array( [ [1.2, 0, 0, 0], [0, 1.2, 0, 0], [0, 0, 1.2, 0], [0, 0, 0, 1], ] ) return arc_data.transform(transform_matrix) def plot_ice_ring(plotter, ice_ring, scalar="Ice thickness"): ice_cmap = plt.get_cmap("Blues", 25) plotter.add_mesh( ice_ring, scalars=scalar, line_width=10, cmap=ice_cmap, clim=[0, 2000], scalar_bar_args={ "title": 'Ice thickness (m)', "position_x": 0.05, "position_y": 0.3, "vertical": True, "title_font_size": 20, "label_font_size": 16, "fmt": "%.0f", "font_family": "arial", } ) # Write ice thicknesss .pvd file ice_thickness = Function(W, name="Ice thickness").interpolate(Hice1 * disc1 + Hice2 * disc2) zero_ice_thickness = Function(W, name="zero").assign(0) # Used for plotting later ice_thickness_file = VTKFile('ice.pvd').write(ice_thickness, zero_ice_thickness) ice_reader = pv.get_reader("ice.pvd") ice_ring = make_ice_ring(ice_reader) reader = pv.get_reader("viscosity.pvd") data = reader.read()[0] # MultiBlock mesh with only 1 block # Create a plotter object plotter = pv.Plotter(shape=(1, 1), border=False, notebook=True, off_screen=False) # Make a colour map boring_cmap = plt.get_cmap("inferno_r", 25) # Add the warped displacement field to the frame plotter.add_mesh( data, component=None, scalars=None, lighting=False, show_edges=False, cmap=boring_cmap, scalar_bar_args={ "title": 'Normalised viscosity', "position_x": 0.8, "position_y": 0.3, "vertical": True, "title_font_size": 20, "label_font_size": 16, "fmt": "%.0f", "font_family": "arial", } ) plot_ice_ring(plotter, ice_ring) plotter.camera_position = 'xy' plotter.show(jupyter_backend="static", interactive=False) # Closes and finalizes movie plotter.close()

Let's setup the timestepping parameters with a timestep of 250 years and an output frequency of 1000 years.

In [13]:

# Timestepping parameters
Tstart = 0
time = Function(R).assign(Tstart * year_in_seconds)

dt_years = 250
dt = Constant(dt_years * year_in_seconds)
Tend_years = 10e3
Tend = Constant(Tend_years * year_in_seconds)
dt_out_years = 1e3
dt_out = Constant(dt_out_years * year_in_seconds)

max_timesteps = round((Tend - Tstart * year_in_seconds) / dt)
log("max timesteps: ", max_timesteps)

output_frequency = round(dt_out / dt)
log("output_frequency:", output_frequency)
log(f"dt: {float(dt / year_in_seconds)} years")
log(f"Simulation start time: {Tstart} years")

# Timestepping parameters Tstart = 0 time = Function(R).assign(Tstart * year_in_seconds) dt_years = 250 dt = Constant(dt_years * year_in_seconds) Tend_years = 10e3 Tend = Constant(Tend_years * year_in_seconds) dt_out_years = 1e3 dt_out = Constant(dt_out_years * year_in_seconds) max_timesteps = round((Tend - Tstart * year_in_seconds) / dt) log("max timesteps: ", max_timesteps) output_frequency = round(dt_out / dt) log("output_frequency:", output_frequency) log(f"dt: {float(dt / year_in_seconds)} years") log(f"Simulation start time: {Tstart} years")

max timesteps:  40
output_frequency: 4
dt: 250.0 years
Simulation start time: 0 years

We can now define the boundary conditions to be used in this simulation. Let's set the bottom and side boundaries to be free slip with no normal flow $\textbf{u} \cdot \textbf{n} =0$. By passing the string ux and uy, G-ADOPT knows to specify these as Strong Dirichlet boundary conditions.

For the top surface we need to specify a normal stress, i.e. the weight of the ice load, as well as indicating this is a free surface.

The delta_rho_fs option accounts for the density contrast across the free surface whether there is ice or air above a particular region of the mantle.

In [14]:

# Setup boundary conditions
exterior_density = rho_ice * (disc1+disc2)
stokes_bcs = {top_id: {'normal_stress': ice_load, 'free_surface': {'delta_rho_fs': density - exterior_density}},
              bottom_id: {'un': 0}
              }

# Setup boundary conditions exterior_density = rho_ice * (disc1+disc2) stokes_bcs = {top_id: {'normal_stress': ice_load, 'free_surface': {'delta_rho_fs': density - exterior_density}}, bottom_id: {'un': 0} }

We also need to specify a G-ADOPT approximation which sets up the various parameters and fields needed for the viscoelastic loading problem.

In [15]:

approximation = SmallDisplacementViscoelasticApproximation(density, shear_modulus, viscosity, g=g)

approximation = SmallDisplacementViscoelasticApproximation(density, shear_modulus, viscosity, g=g)

As noted above, with a free-slip boundary condition on both boundaries, one can add an arbitrary rotation of the form $(-y, x)=r\hat{\mathbf{\theta}}$ to the velocity solution. These lead to null-modes (eigenvectors) for the linear system, rendering the resulting matrix singular. In preconditioned Krylov methods these null-modes must be subtracted from the approximate solution at every iteration. We do that below, setting up a nullspace object, specifying the rotational keyword argument to be True. Note that we do not include a pressure nullspace as the top surface of the model is open.

In [16]:

Z_nullspace = create_stokes_nullspace(Z, closed=False, rotational=True)

Z_nullspace = create_stokes_nullspace(Z, closed=False, rotational=True)

Given the increased computational expense (typically requiring more degrees of freedom) in a 2-D annulus domain, G-ADOPT defaults to iterative solver parameters. As noted in our previous 3-D Cartesian tutorial, G-ADOPT's iterative solver setup is configured to use the GAMG preconditioner for the velocity block of the Stokes system, to which we must provide near-nullspace information, which, in 2-D, consists of two rotational and two translational modes.

In [17]:

Z_near_nullspace = create_stokes_nullspace(Z, closed=False, rotational=True, translations=[0, 1])

Z_near_nullspace = create_stokes_nullspace(Z, closed=False, rotational=True, translations=[0, 1])

We finally come to solving the variational problem, with solver objects for the Stokes system created. We pass in the solution fields z and various fields needed for the solve along with the approximation, timestep and boundary conditions.

In [18]:

stokes_solver = ViscoelasticStokesSolver(z, stress_old, displacement, approximation,
                                         dt, bcs=stokes_bcs, constant_jacobian=True,
                                         nullspace=Z_nullspace, transpose_nullspace=Z_nullspace,
                                         near_nullspace=Z_near_nullspace)

stokes_solver = ViscoelasticStokesSolver(z, stress_old, displacement, approximation, dt, bcs=stokes_bcs, constant_jacobian=True, nullspace=Z_nullspace, transpose_nullspace=Z_nullspace, near_nullspace=Z_near_nullspace)

We next set up our output, in VTK format. This format can be read by programs like pyvista and Paraview.

In [19]:

# Create a velocity function for plotting
velocity = Function(V, name="velocity")
velocity.interpolate(z.subfunctions[0]/dt)
# Create output file
output_file = VTKFile("output.pvd")
output_file.write(*z.subfunctions, displacement, velocity)

plog = ParameterLog("params.log", mesh)
plog.log_str(
    "timestep time dt u_rms u_rms_surf ux_max disp_min disp_max"
)

checkpoint_filename = "viscoelastic_loading-chk.h5"

gd = GeodynamicalDiagnostics(z, density, bottom_id, top_id)

# Initialise a (scalar!) function for logging vertical displacement
U = FunctionSpace(mesh, "CG", 2)  # (Incremental) Displacement function space (scalar)
vertical_displacement = Function(U, name="Vertical displacement")

# Create a velocity function for plotting velocity = Function(V, name="velocity") velocity.interpolate(z.subfunctions[0]/dt) # Create output file output_file = VTKFile("output.pvd") output_file.write(*z.subfunctions, displacement, velocity) plog = ParameterLog("params.log", mesh) plog.log_str( "timestep time dt u_rms u_rms_surf ux_max disp_min disp_max" ) checkpoint_filename = "viscoelastic_loading-chk.h5" gd = GeodynamicalDiagnostics(z, density, bottom_id, top_id) # Initialise a (scalar!) function for logging vertical displacement U = FunctionSpace(mesh, "CG", 2) # (Incremental) Displacement function space (scalar) vertical_displacement = Function(U, name="Vertical displacement")

Now let's run the simulation! At each step we call solve to calculate the incremental displacement and pressure fields. This will update the displacement at the surface and stress values accounting for the time dependent Maxwell consitutive equation.

In [20]:

for timestep in range(max_timesteps+1):

    stokes_solver.solve()

    time.assign(time+dt)

    if timestep % output_frequency == 0:
        # First output step is after one solve i.e. roughly elastic displacement
        # provided dt < maxwell time.
        log("timestep", timestep)

        velocity.interpolate(z.subfunctions[0]/dt)
        output_file.write(*z.subfunctions, displacement, velocity)

        with CheckpointFile(checkpoint_filename, "w") as checkpoint:
            checkpoint.save_function(z, name="Stokes")
            checkpoint.save_function(displacement, name="Displacement")
            checkpoint.save_function(stress_old, name="Deviatoric stress")

    vertical_displacement.interpolate(vertical_component(displacement))

    # Log diagnostics:
    plog.log_str(
        f"{timestep} {float(time)} {float(dt)} "
        f"{gd.u_rms()} {gd.u_rms_top()} {gd.ux_max(top_id)} "
        f"{vertical_displacement.dat.data.min()} "
        f"{vertical_displacement.dat.data.max()} "
    )

for timestep in range(max_timesteps+1): stokes_solver.solve() time.assign(time+dt) if timestep % output_frequency == 0: # First output step is after one solve i.e. roughly elastic displacement # provided dt < maxwell time. log("timestep", timestep) velocity.interpolate(z.subfunctions[0]/dt) output_file.write(*z.subfunctions, displacement, velocity) with CheckpointFile(checkpoint_filename, "w") as checkpoint: checkpoint.save_function(z, name="Stokes") checkpoint.save_function(displacement, name="Displacement") checkpoint.save_function(stress_old, name="Deviatoric stress") vertical_displacement.interpolate(vertical_component(displacement)) # Log diagnostics: plog.log_str( f"{timestep} {float(time)} {float(dt)} " f"{gd.u_rms()} {gd.u_rms_top()} {gd.ux_max(top_id)} " f"{vertical_displacement.dat.data.min()} " f"{vertical_displacement.dat.data.max()} " )

timestep 0

timestep 4

timestep 8

timestep 12

timestep 16

timestep 20

timestep 24

timestep 28

timestep 32

timestep 36

timestep 40

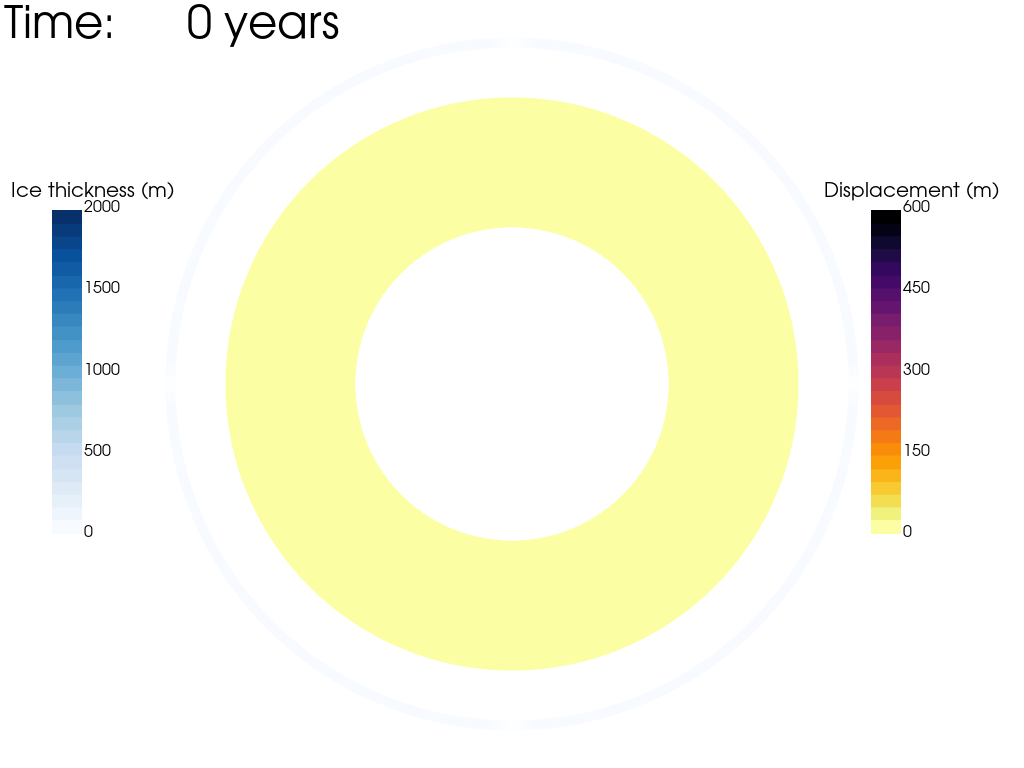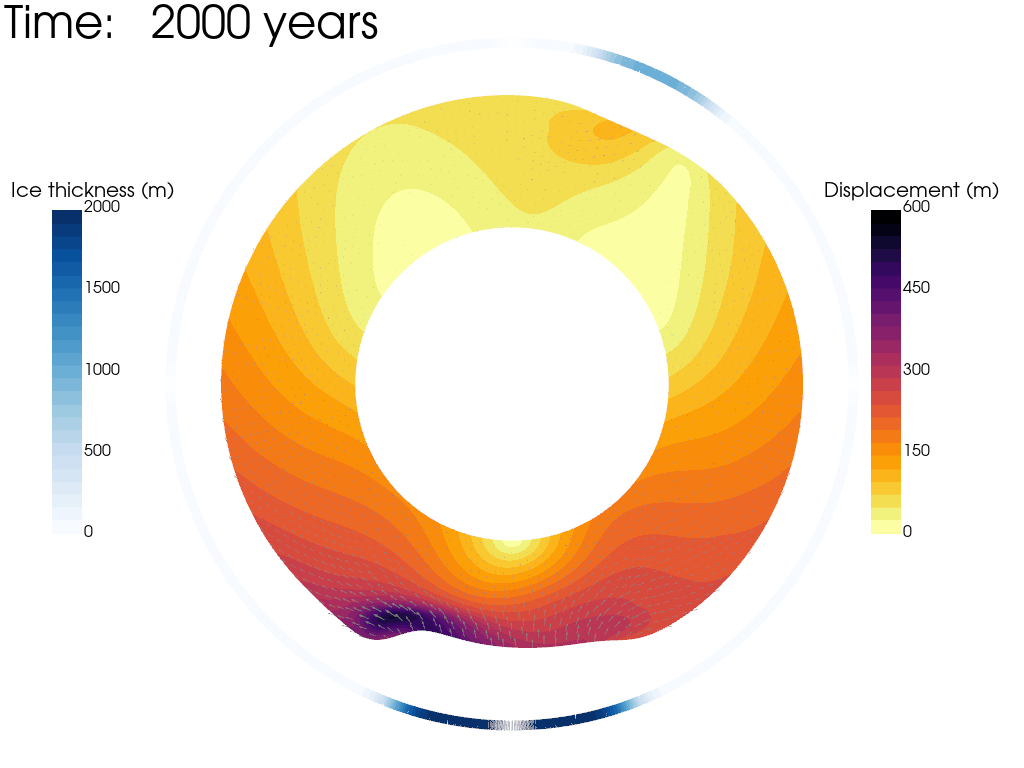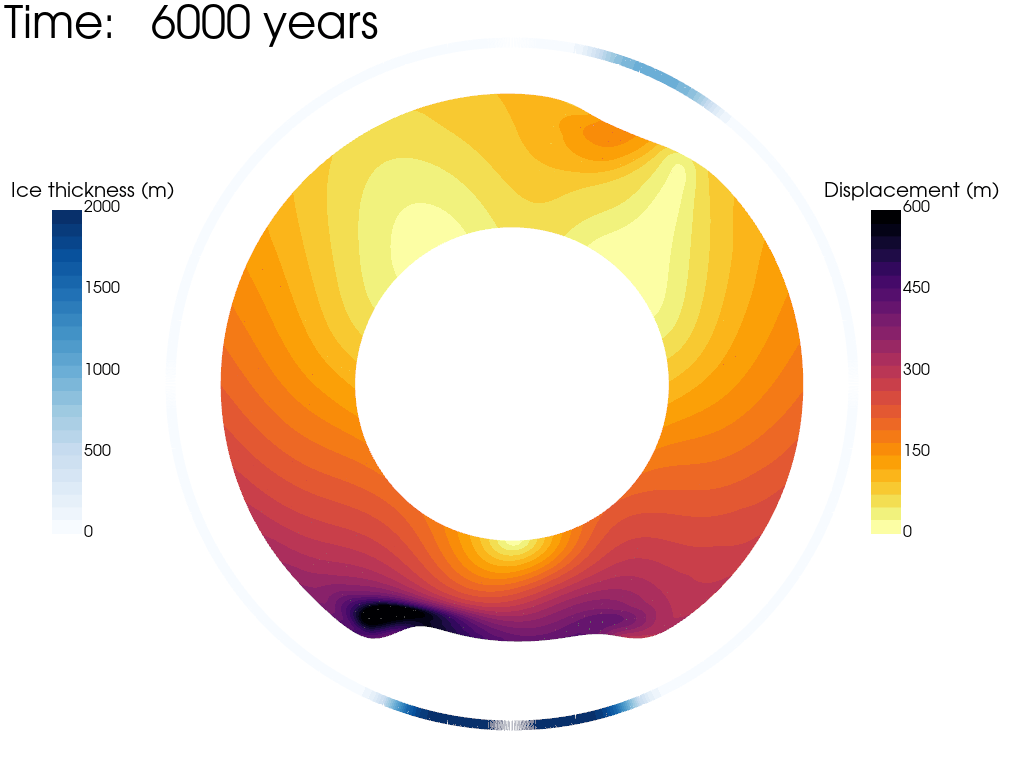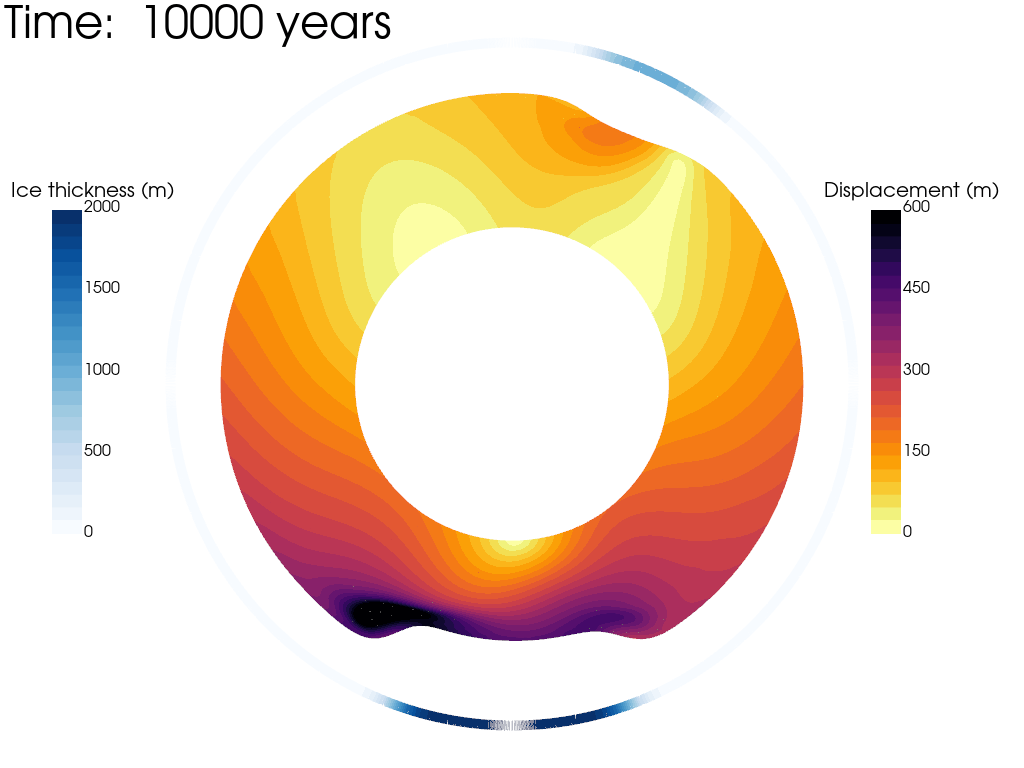
Let's use the python package PyVista to plot the magnitude of the displacement field through time. We will use the calculated displacement to artifically scale the mesh. We have exaggerated the stretching by a factor of 1500, BUT... it is important to remember this is just for ease of visualisation - the mesh is not moving in reality!

In [21]:

active-ipynb

import matplotlib.pyplot as plt
import pyvista as pv

# Read the PVD file
reader = pv.get_reader("output.pvd")
data = reader.read()[0]  # MultiBlock mesh with only 1 block

# Create a plotter object
plotter = pv.Plotter(shape=(1, 1), border=False, notebook=True, off_screen=False)

# Open a gif
plotter.open_gif("displacement_warp.gif")

# Make a colour map
boring_cmap = plt.get_cmap("inferno_r", 25)

# Fix camera in default position otherwise mesh appears to jumpy around!
#plotter.camera_position = 'xy'

# Make a list of output times (non-uniform because also
# outputing first (quasi-elastic) solve
times = [0, dt_years]
for i in range(len(reader.time_values)):
    times.append((i+1)*1000 )


for i in range(len(reader.time_values)):
    print("Step: ", i)
    reader.set_active_time_point(i)
    data = reader.read()[0]
    # Artificially warp the output data in the vertical direction by the free surface height
    # Note the mesh is not really moving!
    warped = data.warp_by_vector(vectors="displacement", factor=1500)
    arrows = warped.glyph(orient="velocity", scale="velocity", factor=1e14, tolerance=0.01)
    plotter.add_mesh(arrows, color="grey", lighting=False)

    # Add the warped displacement field to the frame
    plotter.add_mesh(
        warped,
        scalars="displacement",
        component=None,
        lighting=False,
       # show_edges=True,
        clim=[0, 600],
        cmap=boring_cmap,
        scalar_bar_args={
            "title": 'Displacement (m)',
            "position_x": 0.85,
            "position_y": 0.3,
            "vertical": True,
            "title_font_size": 20,
            "label_font_size": 16,
            "fmt": "%.0f",
            "font_family": "arial",
        }
    )


    plotter.camera_position = [(0, 0, radius_values[0]*5),
                                 (0.0, 0.0, 0.0),
                                 (0.0, 1.0, 0.0)]

    plotter.add_text(f"Time: {times[i]:6} years", name='time-label')

    if i == 0:
        plot_ice_ring(plotter, ice_ring, scalar="zero")
        for j in range(10):
            plotter.write_frame()

    plot_ice_ring(plotter, ice_ring)

    # Write end frame multiple times to give a pause before gif starts again!
    for j in range(10):
        plotter.write_frame()

    if i == len(reader.time_values)-1:
        # Write end frame multiple times to give a pause before gif starts again!
        for j in range(20):
            plotter.write_frame()

    plotter.clear()

# Closes and finalizes movie
plotter.close()

import matplotlib.pyplot as plt import pyvista as pv # Read the PVD file reader = pv.get_reader("output.pvd") data = reader.read()[0] # MultiBlock mesh with only 1 block # Create a plotter object plotter = pv.Plotter(shape=(1, 1), border=False, notebook=True, off_screen=False) # Open a gif plotter.open_gif("displacement_warp.gif") # Make a colour map boring_cmap = plt.get_cmap("inferno_r", 25) # Fix camera in default position otherwise mesh appears to jumpy around! #plotter.camera_position = 'xy' # Make a list of output times (non-uniform because also # outputing first (quasi-elastic) solve times = [0, dt_years] for i in range(len(reader.time_values)): times.append((i+1)*1000 ) for i in range(len(reader.time_values)): print("Step: ", i) reader.set_active_time_point(i) data = reader.read()[0] # Artificially warp the output data in the vertical direction by the free surface height # Note the mesh is not really moving! warped = data.warp_by_vector(vectors="displacement", factor=1500) arrows = warped.glyph(orient="velocity", scale="velocity", factor=1e14, tolerance=0.01) plotter.add_mesh(arrows, color="grey", lighting=False) # Add the warped displacement field to the frame plotter.add_mesh( warped, scalars="displacement", component=None, lighting=False, # show_edges=True, clim=[0, 600], cmap=boring_cmap, scalar_bar_args={ "title": 'Displacement (m)', "position_x": 0.85, "position_y": 0.3, "vertical": True, "title_font_size": 20, "label_font_size": 16, "fmt": "%.0f", "font_family": "arial", } ) plotter.camera_position = [(0, 0, radius_values[0]*5), (0.0, 0.0, 0.0), (0.0, 1.0, 0.0)] plotter.add_text(f"Time: {times[i]:6} years", name='time-label') if i == 0: plot_ice_ring(plotter, ice_ring, scalar="zero") for j in range(10): plotter.write_frame() plot_ice_ring(plotter, ice_ring) # Write end frame multiple times to give a pause before gif starts again! for j in range(10): plotter.write_frame() if i == len(reader.time_values)-1: # Write end frame multiple times to give a pause before gif starts again! for j in range(20): plotter.write_frame() plotter.clear() # Closes and finalizes movie plotter.close()

Step:  0

Step:  1

Step:  2

Step:  3

Step:  4

Step:  5

Step:  6

Step:  7

Step:  8

Step:  9

Step:  10

Step:  11

Looking at the animation, we can see that the weight of the ice load deforms the mantle, sinking beneath the ice load and pushing up material away from the ice load. This forebulge grows through the simulation and by 10,000 years is close to isostatic equilibrium. As the ice load is applied instantaneously the highest velocity occurs within the first timestep and gradually decays as the simulation goes on, though there is still a small amount of deformation ongoing after 10,000 years. We can also clearly see that the lateral viscosity variations give rise to assymetrical displacement patterns. This is especially true near the South Pole, where the low viscosity region has enabled the isostatic relaxation to happen much faster than the surrounding regions.